5. Taking integrals

There is no “direct” support for integrals in lsqfitgp. There’s not something like a deriv=-1 option for GP.addx(). However, since the data can be specified for the derivative of the process, it is possible to do integrals by defining the process for the integral and then fitting its derivative.

Let’s compute the primitive of our dear friend cosine:

import lsqfitgp as lgp
import numpy as np
import gvar

x = np.linspace(-5, 5, 11)
y = np.cos(x)
xplot = np.linspace(-5, 5, 200)

gp = lgp.GP(lgp.ExpQuad(scale=2))
gp.addx(xplot, 'integral')
gp.addx(x, 'cosine', deriv=1)

yplot = gp.predfromdata({'cosine': y}, 'integral')

We just gave the data for the 'cosine' label which has deriv=1, and asked for the posterior on the label 'integral' which is not derived. Now we plot:

from matplotlib import pyplot as plt

fig, ax = plt.subplots(num='lsqfitgp example')

ax.plot(x, y, '.k')
for sample in gvar.raniter(yplot, 8):
    ax.plot(xplot, sample, color='blue', alpha=0.5, zorder=-1)

fig.savefig('integrals1.png')

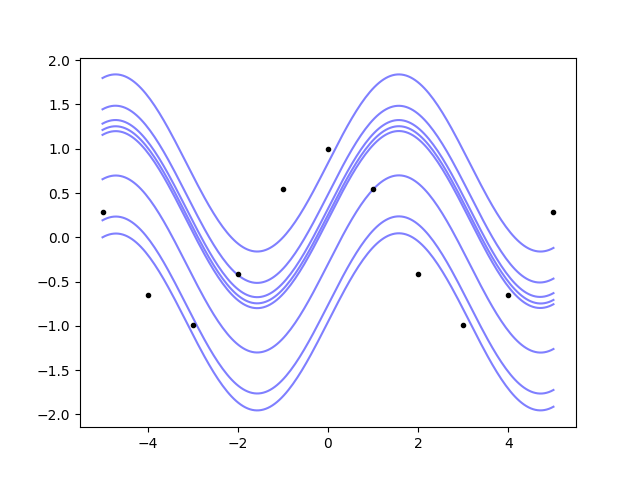
So, the Gaussian process not only can do integrals, it also understands that the primitive is defined up to an additive constant.

How can we do a definite integral? There’s the easy way, and the easy but not obvious way. Let’s go first with the easy one: we will just use the correlation tracking features of gvar.

area = yplot[-1] - yplot[0] # -1 means the last index
print(area)

Output: -1.9157(27). The (27) is a short notation for saying that the standard deviation is 0.0027. Is it correct? Well we know the answer here:

true_area = np.sin(xplot[-1]) - np.sin(xplot[0])
print(true_area, area - true_area)

Output: -1.917848549326277 0.0022(27). So it’s correct within one standard deviation.

The not obvious way follows:

transf = np.zeros_like(xplot)
transf[0] = -1
transf[-1] = 1
gp.addtransf({'integral': transf}, 'definite-integral')
area = gp.predfromdata({'cosine': y}, 'definite-integral')
print(area)

Output: -1.9157(27). What did we do? addtransf() is similar to addx(), but instead of adding new points where the process is evaluated, it adds a linear transformation of already specified process values. The first argument is {'integral': transf}: a dictionary where keys are labels to be transformed, and values are vectors or matrices. In this case we passed a vector, so the transformation is the scalar product of the transf array with the process values we labeled 'integral'. If you look at how we filled transf, you’ll notice that all this is just subtracting the first value from the last.

Using addtransf() for this is an overkill, since transformations applied to the posterior can always be applied directly to the arrays returned by predfromdata(). It becomes useful when there’s data to fit against the transformed quantities.

Example: you already know the area of the function. Let’s try this with a Gaussian:

gaussian = lambda x: 1 / np.sqrt(2 * np.pi) * np.exp(-1/2 * x**2)

x = np.array([-5, -4, -3, -2, 2, 3, 4, 5])
y = gaussian(x)

gp = lgp.GP(lgp.ExpQuad(scale=2))
gp.addx(x, 'datapoints', deriv=1)
gp.addx(-5, 'left')
gp.addx(5, 'right')
gp.addtransf({'left': -1, 'right': 1}, 'area')

xplot = np.linspace(-5, 5, 200)
gp.addx(xplot, 'plot', deriv=1)

yplot = gp.predfromdata({'datapoints': y, 'area': 1}, 'plot')

ax.cla()

for sample in gvar.raniter(yplot, 4):
    ax.plot(xplot, sample, color='blue', alpha=0.5)
ax.plot(xplot, gaussian(xplot), color='gray', linestyle='--')
ax.plot(x, y, '.k')

fig.savefig('integrals2.png')

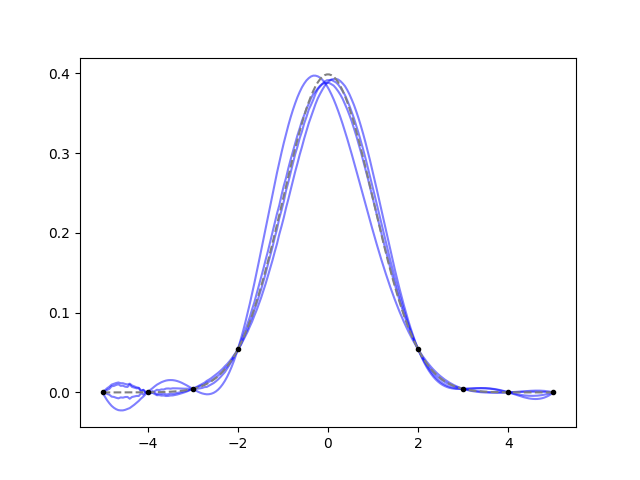
It works well, it draws a Gaussian. However, had we picked an ugly function that is asymmetrical between -2 and 2, the fit would have given the same answer. As usual, the choice of the kernel is important for the result: apparently an exponential quadratic kernel with scale=2 likes Gaussians.