10. Splitting components

In More on kernels we saw an example where we summed two ExpQuad kernels with different scale, and the result effectively looked like the sum of two processes, because the kernel of a sum of processes is the sum of their kernels.

When summing processes it is useful to get the fit result separately for each component. We first generate some data:

import numpy as np
import lsqfitgp as lgp
import gvar
from matplotlib import pyplot as plt

kernel_long = 10 * lgp.ExpQuad(scale=10)
kernel_short = lgp.ExpQuad(scale=1)

x = np.linspace(-10, 10, 21)
fakedata = {}
fakedata['long'] = gvar.sample(lgp.GP(kernel_long).addx(x, 'A').prior('A'))
fakedata['short'] = gvar.sample(lgp.GP(kernel_short).addx(x, 'A').prior('A'))
fakedata['sum'] = fakedata['long'] + fakedata['short']

fig, ax = plt.subplots(num='lsqfitgp example')

ax.plot(x, fakedata['sum'], '.k')

fig.savefig('components1.png')

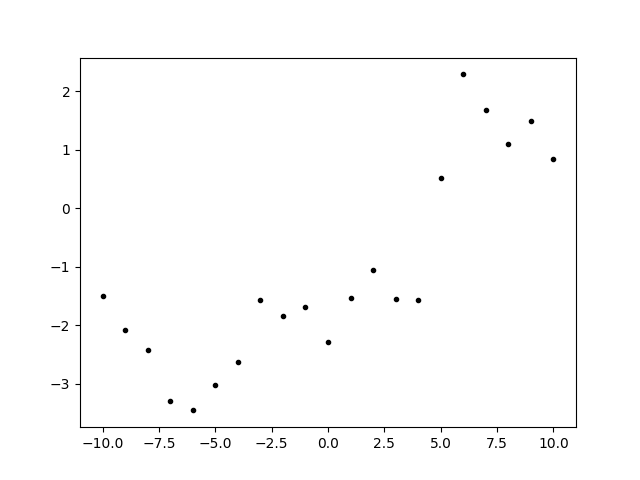
We defined two processes with different correlation lengths, sampled from each, and summed the result to make our fake data. Generating fake data from the prior is a good way to test a statistical procedure.

We also saved the data generated for each component. Our goal is to recover the components by using only the sum. We start by creating a GP object without specifying a kernel:

gp = lgp.GP()

Then we add separately the two kernels to the object using GP.defproc:

gp = (gp
    .defproc('long', kernel_long)
    .defproc('short', kernel_short)
)

Now the two names 'long' and 'short' stand for a priori independent processes with their respective kernels. These names reside in a namespace separate from the one used by addx, addlintransf, etc. Now we use these to define the sum as a process:

gp = gp.deflintransf('sum',
    lambda l, s: lambda x: l(x) + s(x),
    ['long', 'short'])

The method deflintransf is analogous to addlintransf but works for a whole process at once. What we are doing mathematically is the following:

\[\operatorname{sum}(x) \equiv \operatorname{long}(x) + \operatorname{short}(x).\]

The second argument to the method is a function that takes in two functions, and outputs a new function. The third argument specifies which processes are to be transformed in such way.

Now that we have defined all the processes we care about, we evaluate them on the points:

xplot = np.linspace(-10, 10, 200)

gp = (gp
    .addx(x, 'datalong' , proc='long' )
    .addx(x, 'datashort', proc='short')
    .addx(x, 'datasum'  , proc='sum'  )

    .addx(xplot, 'plotlong' , proc='long' )
    .addx(xplot, 'plotshort', proc='short')
    .addx(xplot, 'plotsum'  , proc='sum'  )
)

We specified the processes using the proc parameter of addx. Then we continue as usual:

post = gp.predfromdata({
    'datasum': fakedata['sum'],
}, ['plotlong', 'plotshort', 'plotsum'])

ax.cla()

for sample in gvar.raniter(post, 2):
    line, = ax.plot(xplot, sample['plotsum'])
    color = line.get_color()
    ax.plot(xplot, sample['plotlong'], '--', color=color)
    ax.plot(xplot, sample['plotshort'], ':', color=color)

for marker, key in zip(['x', '+', '.'], ['long', 'short', 'sum']):
    ax.plot(x, fakedata[key], color='black', marker=marker, label=key, linestyle='')
ax.legend()

fig.savefig('components4.png')

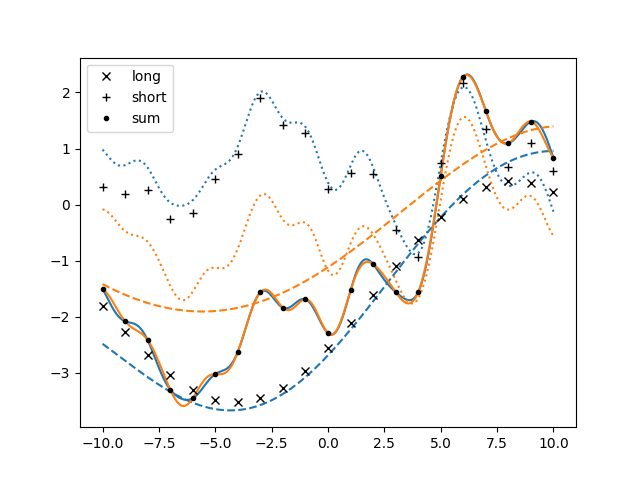
GP.defproc can only define a priori independent processes. To have a priori correlations it would be necessary to define a single process over an extended input, with an explicit index indicating the component, such that the kernel can act on it. We did this at the end of Multidimensional output when we introduced an anticorrelation between the random walk components by multiplying the kernel with lgp.Categorical(dim='coord', cov=[[1, -0.99], [-0.99, 1]]).