5. Taking integrals¶
There is no “direct” support for integrals in lsqfitgp. There’s not
something like a deriv=-1 option for GP.addx(). However, since the
data can be specified for the derivative of the process, it is possible to do
integrals by defining the process for the integral and then fitting its
derivative.
Let’s compute the primitive of our dear friend cosine:
import lsqfitgp as lgp
import numpy as np
import gvar
x = np.linspace(-5, 5, 11)
y = np.cos(x)
xplot = np.linspace(-5, 5, 200)
gp = lgp.GP(lgp.ExpQuad(scale=2))
gp.addx(xplot, 'integral')
gp.addx(x, 'cosine', deriv=1)
yplot = gp.predfromdata({'cosine': y}, 'integral')
We just gave the data for the 'cosine' label which has deriv=1, and
asked for the posterior on the label 'integral' which is not derived. Now
we plot:
from matplotlib import pyplot as plt
fig, ax = plt.subplots(num='lsqfitgp example')
ax.plot(x, y, '.k')
for sample in gvar.raniter(yplot, 8):
ax.plot(xplot, sample, color='blue', alpha=0.5, zorder=-1)
fig.savefig('integrals1.png')
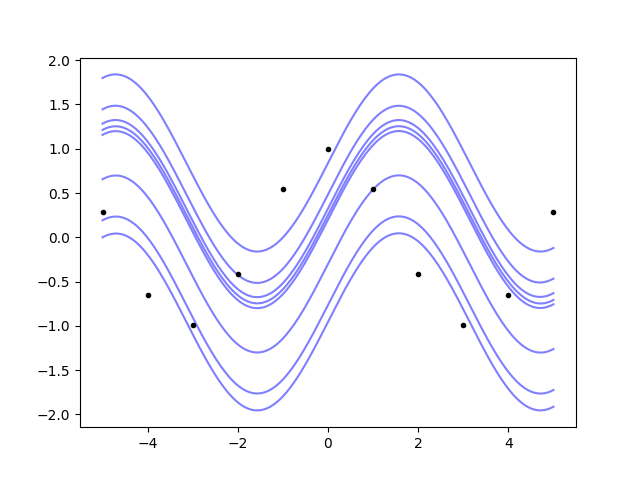
So, the Gaussian process not only can do integrals, it also understands that the primitive is defined up to an additive constant.
How can we do a definite integral? There’s the easy way, and the easy but not
obvious way. Let’s go first with the easy one: we will just use the correlation
tracking features of gvar.
area = yplot[-1] - yplot[0] # -1 means the last index
print(area)
Output: -1.9157(27). The (27) is a short notation for saying that the
standard deviation is 0.0027. Is it correct? Well we know the answer here:
true_area = np.sin(xplot[-1]) - np.sin(xplot[0])
print(true_area, area - true_area)
Output: -1.917848549326277 0.0022(27). So it’s correct within one standard
deviation.
The not obvious way follows:
transf = np.zeros_like(xplot)
transf[0] = -1
transf[-1] = 1
gp.addtransf({'integral': transf}, 'definite-integral')
area = gp.predfromdata({'cosine': y}, 'definite-integral')
print(area)
Output: -1.9157(27). What did we do? addtransf() is similar to
addx(), but instead of adding new points where the process is
evaluated, it adds a linear transformation of already specified process values.
The first argument is {'integral': transf}: a dictionary where keys are
labels to be transformed, and values are vectors or matrices. In this case we
passed a vector, so the transformation is the scalar product of the transf
array with the process values we labeled 'integral'. If you look at how
we filled transf, you’ll notice that all this is just subtracting the
first value from the last.
Using addtransf() for this is an overkill, since transformations
applied to the posterior can always be applied directly to the arrays returned
by predfromdata(). It becomes useful when there’s data to fit against
the transformed quantities.
Example: you already know the area of the function. Let’s try this with a Gaussian:
gaussian = lambda x: 1 / np.sqrt(2 * np.pi) * np.exp(-1/2 * x**2)
x = np.array([-5, -4, -3, -2, 2, 3, 4, 5])
y = gaussian(x)
gp = lgp.GP(lgp.ExpQuad(scale=2))
gp.addx(x, 'datapoints', deriv=1)
gp.addx(-5, 'left')
gp.addx(5, 'right')
gp.addtransf({'left': -1, 'right': 1}, 'area')
xplot = np.linspace(-5, 5, 200)
gp.addx(xplot, 'plot', deriv=1)
yplot = gp.predfromdata({'datapoints': y, 'area': 1}, 'plot')
ax.cla()
for sample in gvar.raniter(yplot, 4):
ax.plot(xplot, sample, color='blue', alpha=0.5)
ax.plot(xplot, gaussian(xplot), color='gray', linestyle='--')
ax.plot(x, y, '.k')
fig.savefig('integrals2.png')
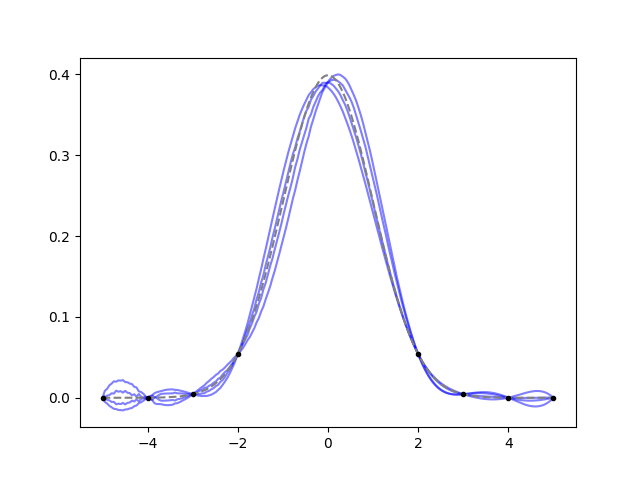
It works well, it draws a Gaussian. However, had we picked an ugly function
that is asymmetrical between -2 and 2, the fit would have given the same
answer. As usual, the choice of the kernel is important for the result:
apparently an exponential quadratic kernel with scale=2 likes Gaussians.